Applicazioni del Teorema di Bayes
Il Teorema di Bayes è uno strumento potente che trova applicazioni in diverse aree, dalla statistica alla medicina. In sostanza, ci permette di aggiornare le nostre credenze sulla base di nuove informazioni. È come quando vedi un amico che indossa un cappotto pesante e deduci che probabilmente fa freddo fuori.
Inferenza Statistica
L’inferenza statistica si occupa di trarre conclusioni su una popolazione basandosi su un campione di dati. Il teorema di Bayes ci aiuta a calcolare la probabilità di un’ipotesi data l’evidenza osservata. Ad esempio, se vogliamo stimare la probabilità che un paziente abbia una certa malattia, possiamo usare il teorema di Bayes per combinare la probabilità a priori della malattia con la probabilità di osservare i sintomi del paziente.
Apprendimento Automatico
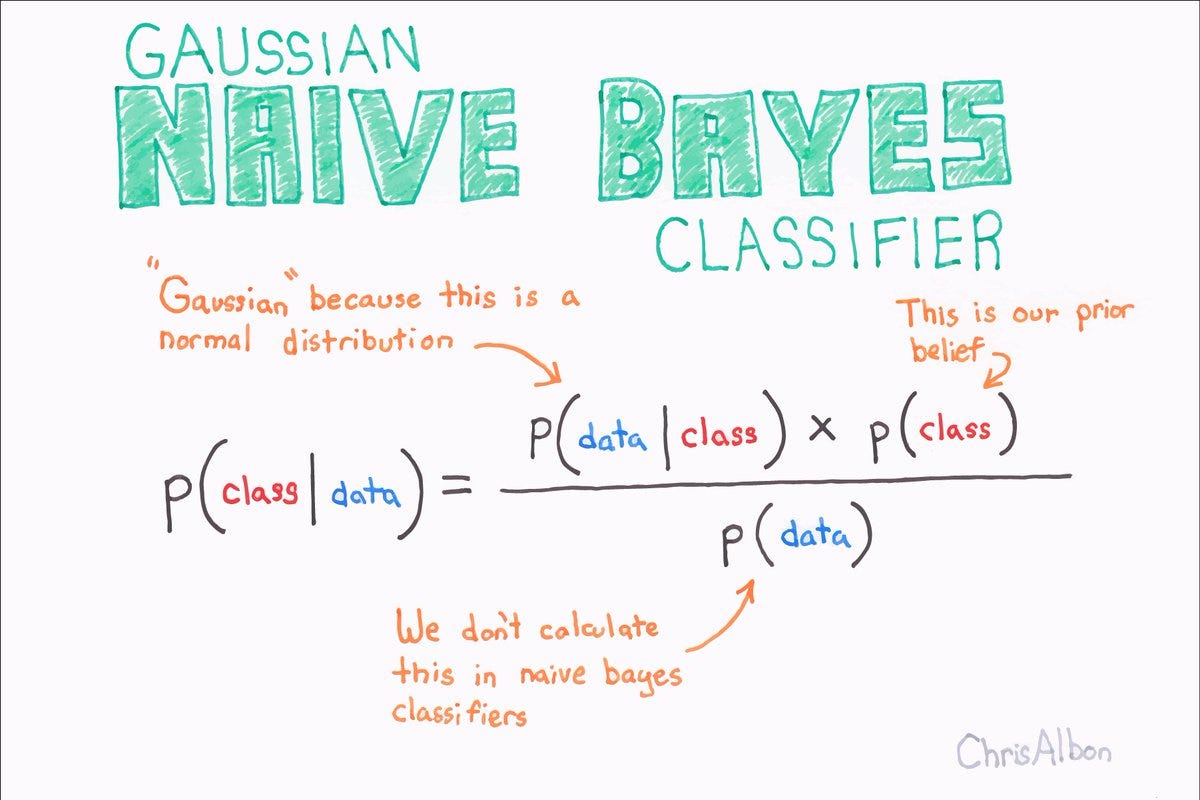
L’apprendimento automatico si basa sull’idea di far imparare ai computer dai dati. Il teorema di Bayes è fondamentale per algoritmi di classificazione, come i classificatori Bayesiani Naïve. Questi algoritmi usano il teorema di Bayes per prevedere la classe di un nuovo dato in base alle informazioni contenute nei dati di training. Ad esempio, possiamo usare un classificatore Bayesiano Naïve per prevedere se un cliente è propenso ad acquistare un prodotto in base alle sue informazioni demografiche e al suo comportamento di acquisto.
Medicina
In medicina, il teorema di Bayes viene utilizzato per diagnosticare le malattie. Ad esempio, possiamo usare il teorema di Bayes per calcolare la probabilità che un paziente abbia una certa malattia, data la presenza di determinati sintomi. Questo ci aiuta a prendere decisioni cliniche più accurate e a migliorare la cura del paziente.
Confronto tra approcci Bayesiani e Frequentisti
| Aspetto | Approccio Bayesiano | Approccio Frequentista |
|---|---|---|
| Interpretazione della probabilità | Grado di credenza | Frequenza relativa a lungo termine |
| Informazione a priori | Utilizzata | Non utilizzata |
| Stima dei parametri | Distribuzione di probabilità | Valori puntuali |
| Inferenza | Aggiornamento delle credenze | Test di ipotesi |
Concetti correlati: Bayesian

Il teorema di Bayes è un potente strumento per l’analisi statistica, ma per capirlo a fondo, è necessario comprendere alcuni concetti correlati. Questi concetti forniscono il contesto necessario per applicare correttamente il teorema e interpretare i risultati.
Probabilità a priori e probabilità a posteriori
La probabilità a priori, o probabilità iniziale, è la probabilità di un evento prima che si verifichi un nuovo dato. Ad esempio, la probabilità a priori che un dado esca con un 6 è 1/6. La probabilità a posteriori, o probabilità aggiornata, è la probabilità di un evento dopo che si è verificato un nuovo dato. Ad esempio, se si lancia un dado e si osserva che è uscito un numero pari, la probabilità a posteriori che sia uscito un 6 diventa 1/3, perché ora sappiamo che il risultato deve essere uno dei numeri pari (2, 4 o 6).
Il teorema di Bayes ci permette di calcolare la probabilità a posteriori di un evento dato un nuovo dato, utilizzando la probabilità a priori, la probabilità di osservare il nuovo dato e la probabilità del nuovo dato dato l’evento.
Inferenza bayesiana e inferenza frequentista
L’inferenza bayesiana è un approccio all’inferenza statistica che utilizza il teorema di Bayes per aggiornare le probabilità di ipotesi in base ai dati osservati. L’inferenza frequentista, invece, si basa sulla frequenza relativa degli eventi in un numero infinito di prove per stimare le probabilità.
La differenza fondamentale tra i due approcci sta nel modo in cui viene trattata l’incertezza. L’inferenza bayesiana considera l’incertezza come una probabilità, mentre l’inferenza frequentista considera l’incertezza come una varianza.
Distribuzione a priori, Bayesian
La distribuzione a priori è una distribuzione di probabilità che rappresenta la nostra conoscenza a priori di un evento. In altre parole, è la nostra migliore ipotesi sulla probabilità di un evento prima che si verifichi un nuovo dato. La distribuzione a priori può essere informativa, ovvero basata su dati precedenti o su una conoscenza esperta, o non informativa, ovvero basata su un’ipotesi di probabilità uniforme.
La distribuzione a priori influenza la probabilità a posteriori. Una distribuzione a priori informativa può portare a una probabilità a posteriori più precisa, mentre una distribuzione a priori non informativa può portare a una probabilità a posteriori meno precisa.
Bayesian statistics, like a good surf session, is all about updating your knowledge as you get more data. It’s like how Mike Lynch, the legendary running back , would adjust his game plan based on the opponent’s moves. Bayesian analysis, in a nutshell, is about using prior knowledge to make better predictions, just like a seasoned surfer reading the waves.
Bayesian thinking, it’s all about understanding the probability of something happening based on what you already know. Like, imagine you’re cruising around on a Perini Navi yacht, and you see a dolphin jumping. Bayesian logic helps you figure out how likely it is to see another dolphin based on that initial sighting.
It’s all about making smart decisions based on the information you have, just like choosing the perfect spot to anchor your luxury yacht.
